The Gringarten-Bourdet Type Curve describes the pressure for a vertical well with constant WBS and skin in an infinite-acting reservoir.
The dimensionless pressure-derivative function \(P'_D\) is plotted as a function of \(t_D/C_D\) for various values of the correlating parameter \(C_De^{2s}\)
The \(P_D\) and \(P'_D\) type curves are in a single plot, permiting simultaneous type-curve analysis with both pressure and pressure-derivative curves and reducing the ambiguity.
Interpretation Process
- Field data (\(\Delta P\) and \(\Delta P'\) vs. \(t\) for DD, \(\Delta P\) and \(\Delta P'\) vs. \(\Delta t\) or \(t_e\) for BU ) are plotted on log-log scale
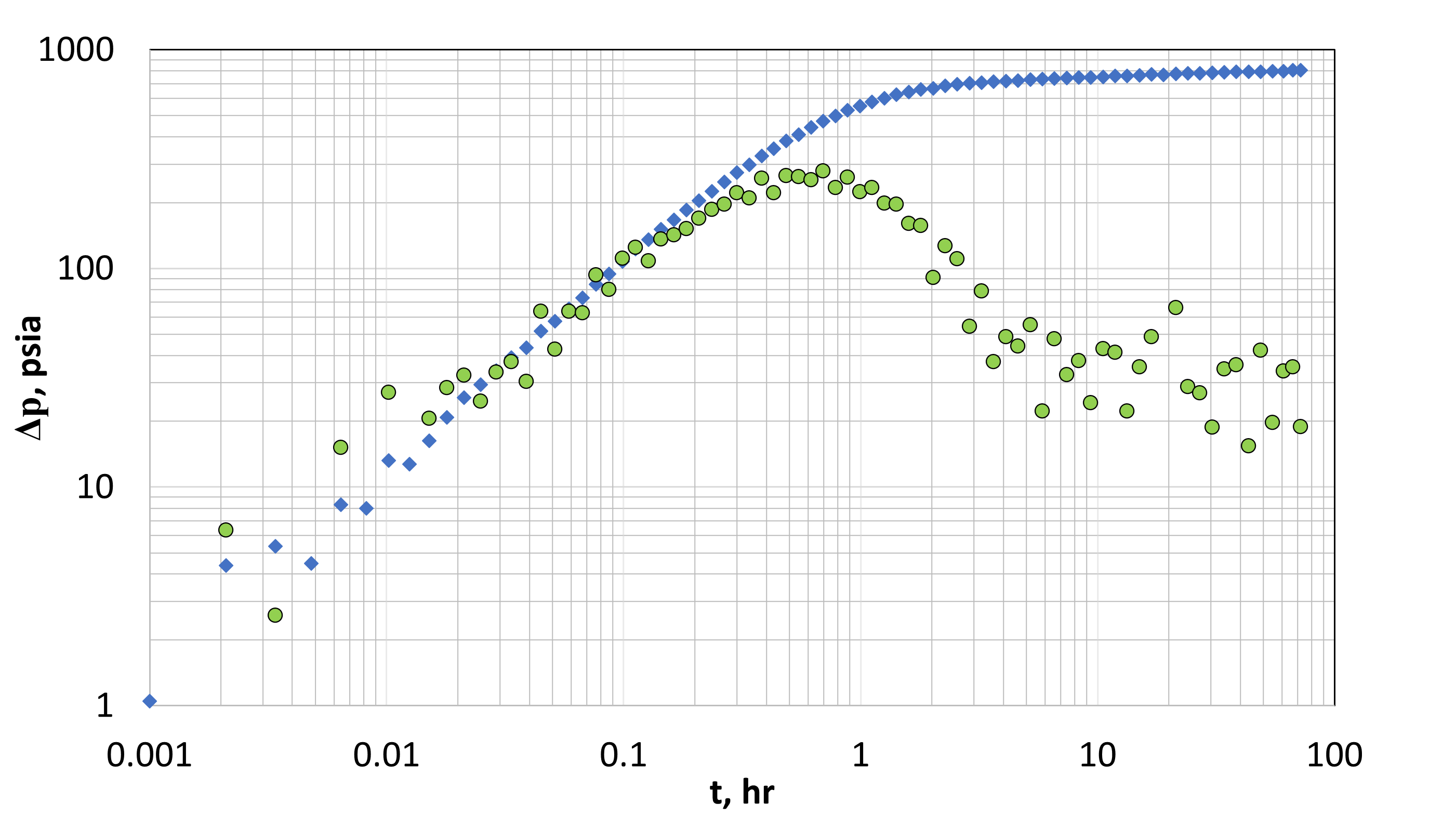
Identify the IARF period indicated by the horizontal portion od the derivative and the WBS-dominated period, indicated by the unit-slope portion of the derivative.
Match the data on the curves, then pick any convenient point (match point, red point)
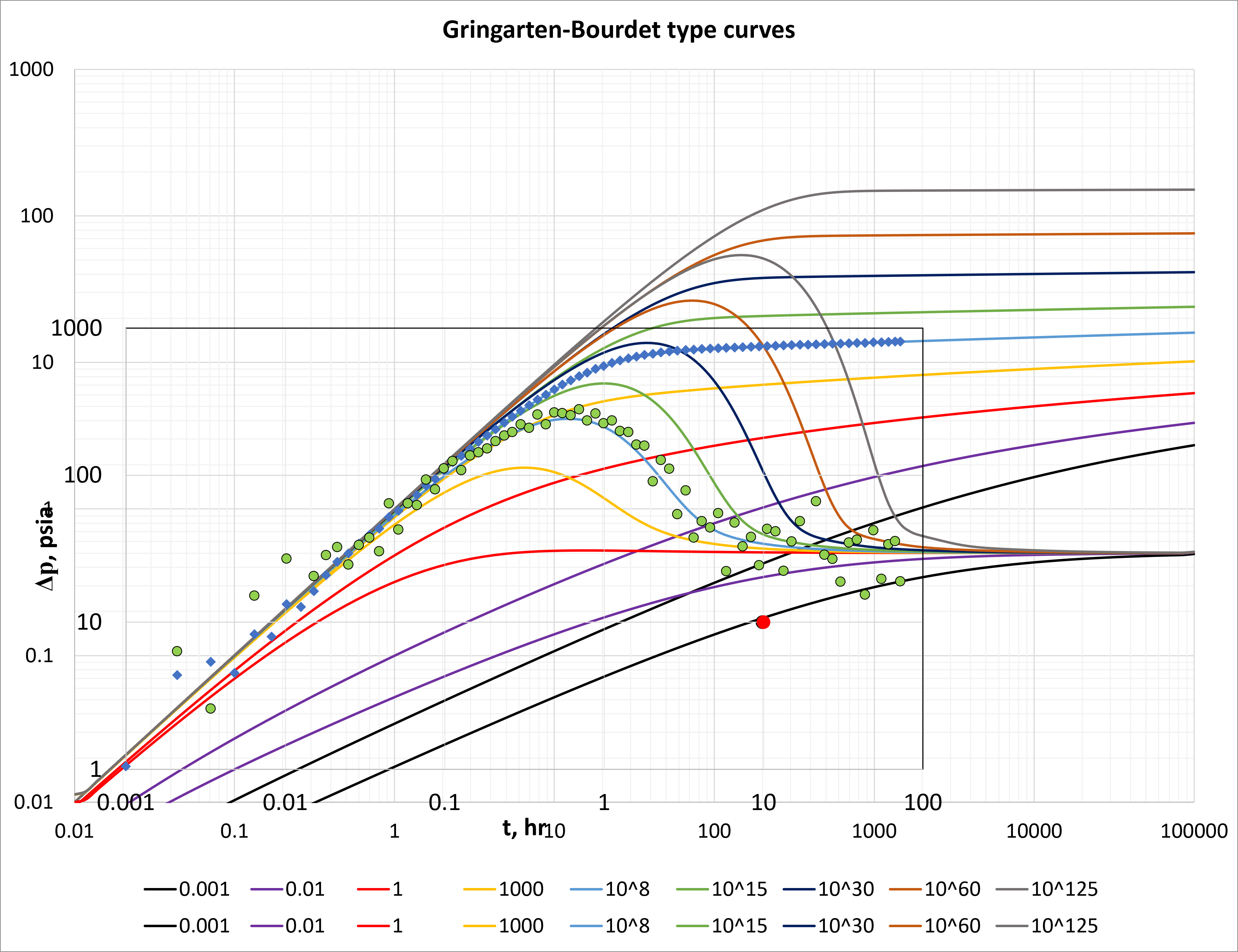
- Read \(\Delta P\) and \(P_D\) corresponding to the match point, read \(t\) and \(t_D/C_D\) corresponding to the match point and read the matching value of \(C_De^{2s}\)
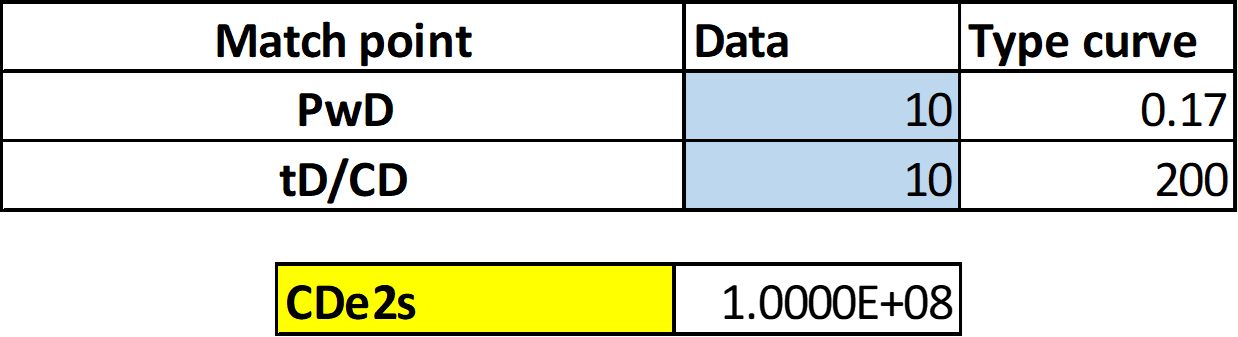
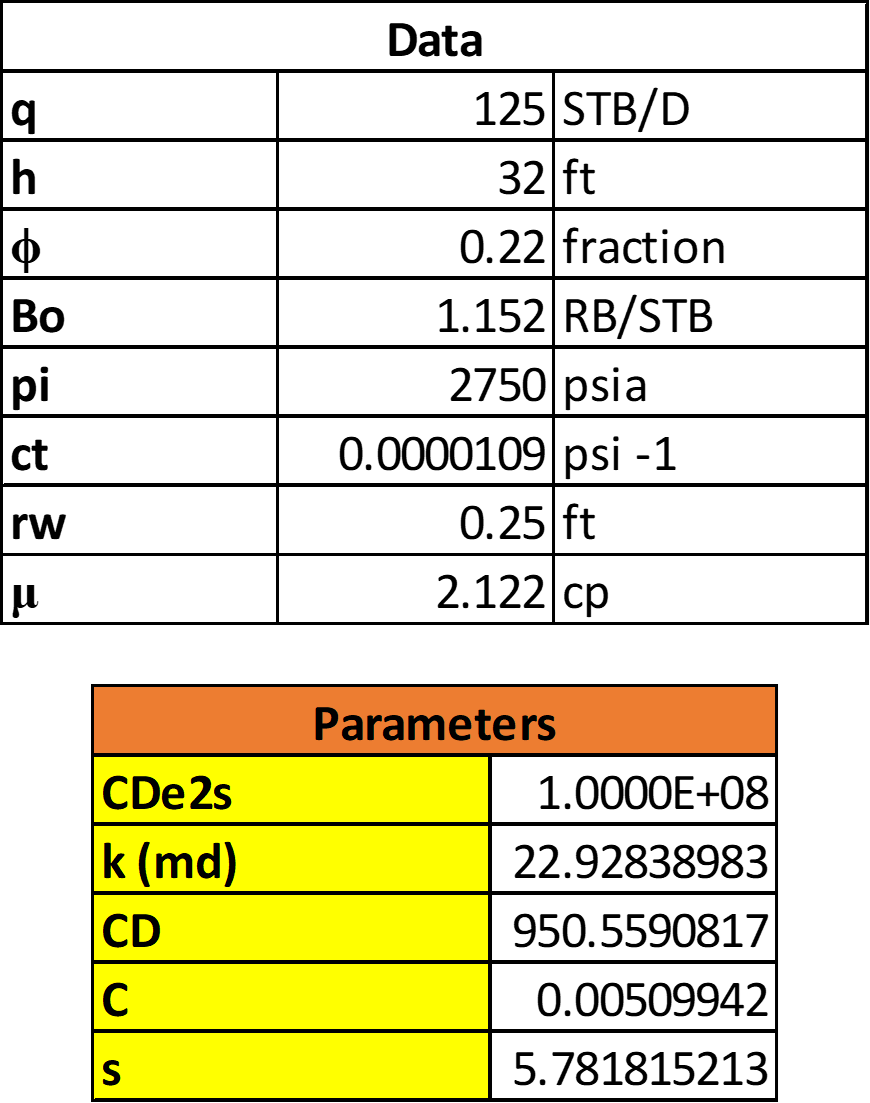
- Calculate well test parameters with the following equations
\[k = \frac{141.2qB \mu}{h} \left(\frac{P_D}{\Delta P}\right)_{MP}\]
\[C_D = \frac{0.0002637k}{\phi\mu c_t r_{w}^2} \left(\frac{t}{t_D/C_D}\right)_{MP}\]
\[C_D = \frac{\phi c_t h r_{w}^2}{0.894} C_D\]
\[s = 0.5ln\left(\frac{C_De^{2s}}{C_D}\right)\]
Example
References
Lee, J. & Spivey, J. (2013) Applied Well Test Interpretation using the recommended procedure