Fetkovich (1980) developed a set of dimensionaless (log-log) type curves for production data (rate-time) analysis of wells completed in conventional reservoir.
The fetkovich type curves were developed specifically to analize vertical wells exhibiting transient flow followed by boundary-dominated flow for the case of a well placed at the center of a closed cylindrical reservoir. In order to incorporate the effects of near-wellbore stimulation/damage effects, the apparent (efective) radius concept was employed in type-curve development.
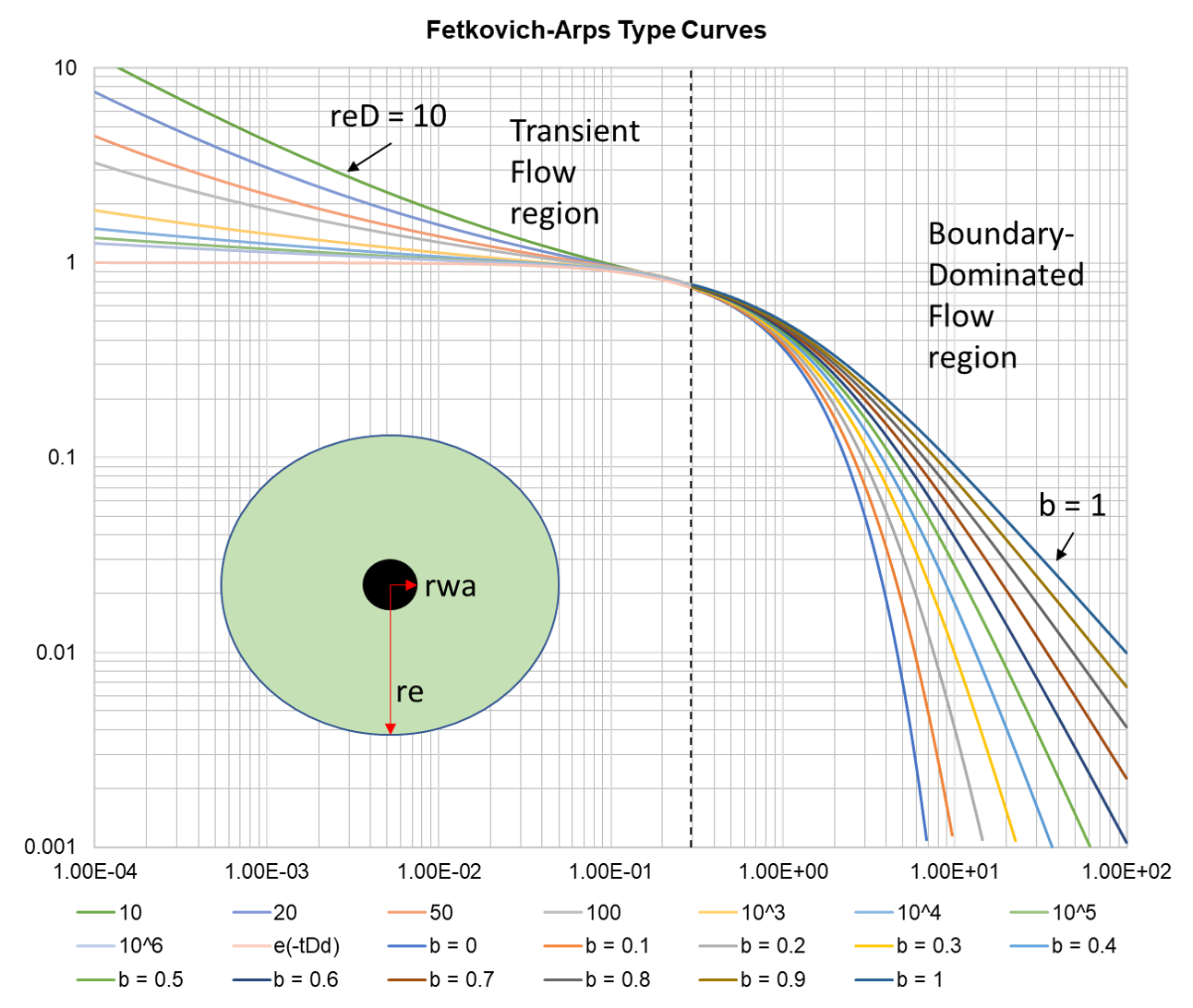
The left part when \(t_{Dd} < 0.3\) represents the early and middle transient flow period, which is mainly affected by dimensionless reservoir drainage radius \(r_{eD}\) and the right part when \(t_{Dd} > 0.3\) represents the boundary-dominated flow, which is the curve cluster controlled by Arps decline exponent \(b\)
The solution for constant BHFP for a well entered in a closed circular reservoir could be regarded as an Arps exponential decline curve in the later flow period, it could be described by a general formula:
\[ q_{Dd}(t_{Dd})= \frac{1}{(1+bt_{Dd})^{1/b}} \]
For a well entered in a closed circular reservoir a constant BHFP , the relationship between Fetkovich dimensionless decline rate function qDd and dimensionless decline time tDd is defined as:
\[q_{Dd} = q_D\left[ln \left(\frac{r_e}{r_{wa}}\right)-\frac{1}{2}\right] \] \[ t_{Dd} = \frac{t_D}{\frac{1}{2}\left[\left(\frac{r_e}{r_{wa}}\right)^2-1\right]\left[ln \left(\frac{r_e}{r_{wa}}\right)-\frac{1}{2}\right]}\] \[ r_{eD} = \frac{r_e}{r_{wa}}\]
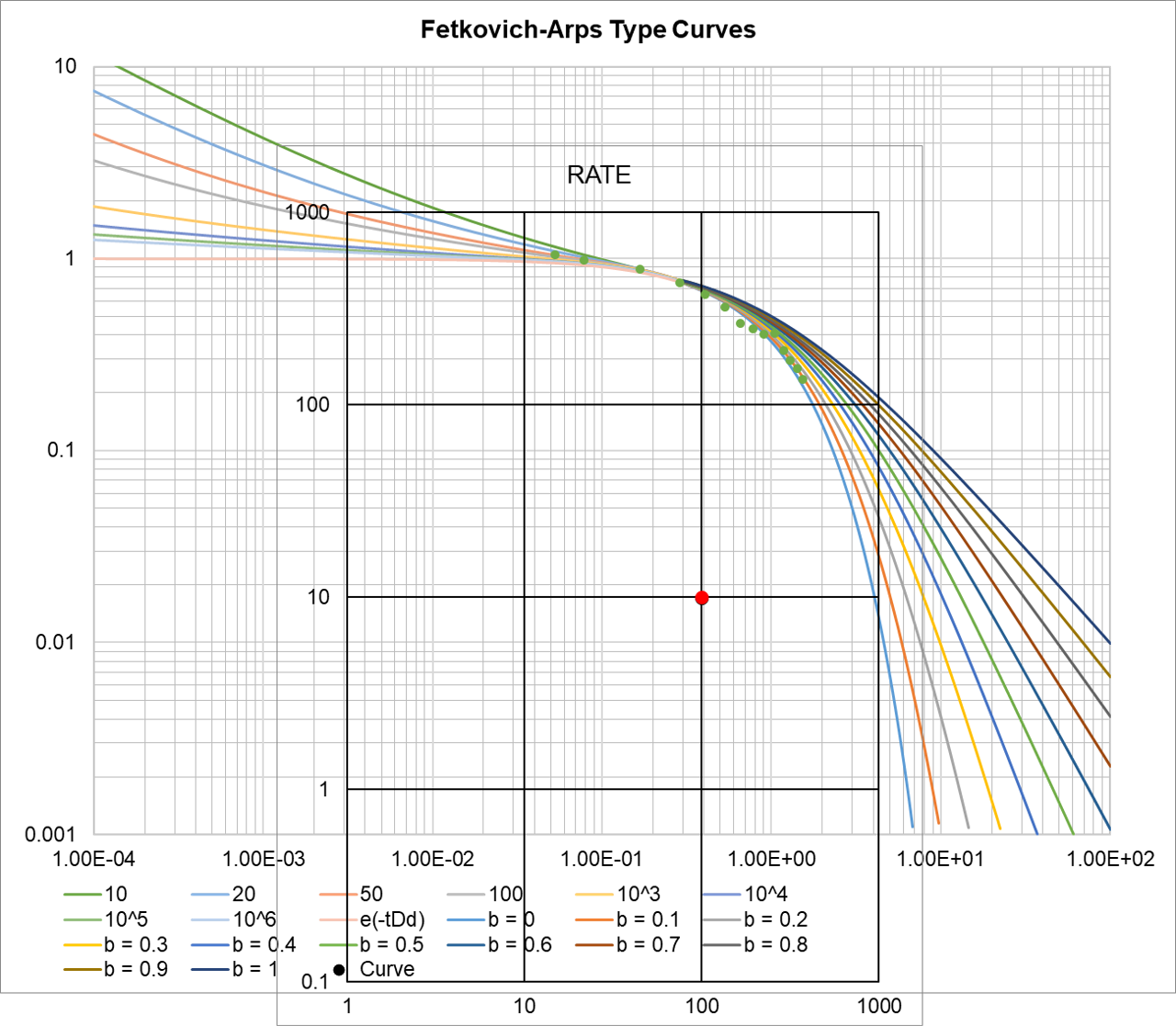
Using the type-curve matching method between field data and Fetkovich-Arps type curve, the Arps decline parameters \(q_i\), \(D_i\) and \(b\) could be determined by the second half of the type curve, and the value of \(r_{eD}\) could be determined by the first half of the curves. Then the permeability \(K\), skin factor \(S\), reservoir drainage radius \(r_e\), single-well original HC in place, ans the cumulative production before reaching the abandoned condition could all be determined.
Determine the initial flow rate
\[q_i=\left(\frac{q}{q_{Dd}}\right)_M\]
Determine the initial decline rate \(D_i\)
\[D_i=\left(\frac{t_{Dd}}{t}\right)_M\]
Acording \(r_{eD}\) value and \(q_i\) determine the value of permeability
\[k = \frac{141.2B_o \mu}{h(p_i-p_{wf})}\left[ln \left(\frac{r_e}{r_{wa}}\right)-0.5\right]\left(\frac{q}{q_{Dd}}\right)_M\]
Calculate the apparent wellbore radius based in the time matching point
\[r_{wa} = \sqrt{\frac{0.00633k}{\phi\mu_o c_t(0.5) \left[ r_{eD}^2-1\right]\left[ln \left(r_{eD}\right)-0.5\right]}\left(\frac{t}{t_{Dd}}\right)_M}\]
and then determine the skin factor \(S\)
\[S = ln\frac{r_w}{r_{wa}}\]
Example

References
Sun, H. (2015) Advanced Production Decline Analysis and Application Clarkson C.R. (2021) Unconventional Reservoir Rate-Transient Analysis